Guardrail Study: Reducing Wear, Reducing Replacements.

Transit systems are typically operated in dense urban areas, which frequently result in systems that contain a large number of curves with small radii that can increase wheel/rail wear and the potential for flange climb derailments. Guardrails are used in transit systems to reduce rail wear in sharp curves and to increase the track’s resistance to flange climb derailment. Guardrails are also installed in track curves where the high rail wears rapidly, because they are considered beneficial in reducing the frequency and cost of high rail replacements.

Survey results published by the Transit Cooperative Research Program (TCRP) show that thepractices of restraining rail installation are different and the design and maintenance standards vary between different transit systems. This wide variety of practices coupled with problems observed in the use of the guard/restraining rails, indicated that a detailed study of restraining rail designs and maintenance practices could be beneficial to all transit systems.

The Transportation Technology Center Inc. (TTCI) worked with TCRP to develop guidelines for the application of guard/restraining rails in transit systems, including comparisons of the following two guardrail installation designs (referred to as philosophies I and II) commonly used in transit systems.

Figure 1 illustrates the “shared contact” methodology used by transit systems for guardrail installation, known as philosophy I. The optimization methodology proposed in the previous study for optimal flangeway clearance clearly belongs to philosophy I. With equal rates of wear, it is expected that the high rail and the guard/girder/restraining rail will wear out at the same time and be replaced during the same track maintenance period, minimizing service interruptions.

As Figure 2 illustrates, there is a different guardrail installation philosophy used by transit systems, known as philosophy II. The practice of philosophy II is to increase the check gage dimension and track gage so that no flange contact with the high rail will occur under any combination of wear and tolerances. Then the guard/girder/restraining rail resists all the curving forces, and therefore experiences all the gage-face wear while the high rail experiences only rail head wear.

Even though the wheel/rail contact of these two philosophies starts in two significantly different situations, they ultimately end with the same situation as philosophy I, because the high rail contact will eventually occur for philosophy II as the guard/restraining rail gradually wears.

Which philosophy is right for installing a guardrail? To answer this, the effects of guardrail parameters on dynamic performances of various types of transit vehicles were investigated through NUCARS modeling.

EFFECT OF GUARDRAIL PARAMETER AND OPTIMIZATION

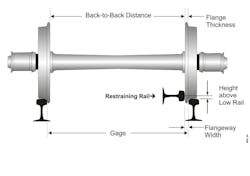
Figures 3 and 4 show typical guardrail and restraining rail structures and layouts. The geometry parameters of wheelset and track including guard/restraining rail are also labeled in the figures. The restraining rail contacts the wheel flange back flat surface with a 90-degree contact angle; the contact angle between the guardrail and wheel flange back tip depends on the rail and wheel profile shape; usually it is less than 90 degrees. The flangeway width has the most important effect on wheel/rail forces and wear.

As Figure 5 shows, for a 75-degree flange angle wheel with a 20 milliradian (mrad) yaw angle, if the flangeway width is too narrow (smaller or equal to 1.5 in.), the guardrail bears almost all the lateral force, and there is no lateral force acting on the high rail (right rail). Correspondingly, the left wheel wears severely on the guardrail, but the right wheel wear index is relatively small on the high rail tread and flange, as Figure 6 shows.

The guardrail and fastener components could be damaged from the high lateral force. The guardrail service life could also be reduced from severe wear. The optimal flangeway width is 1.55 inches for the simulated case.